In the UK, there is a popular gameshow called Countdown . The main thrust of the programme is to try to create the longest word from a randomly set of vowels and consonants pulled from two stacks of jumbled letters. Contestants get points for the length of the validated words and the individual with the most points - wins. For some light relief, there is a “Numbers Round”. In this round the contestants are presented with six initial numbers and are given a target to reach. The six initial numbers are split into two groups; small numbers, between 1 and 10; large numbers, 25, 50, 75, or 100. Instead of pulling from stack, there is a board containing 20 small numbers (2 of each option) and one of each of the large numbers. The contestant driving the round requests, for example, 2 large and 4 small and are presented with a legal combination based on the rules above. A random number is then generated between 1 and 999, which may or may not be possible, and the contestants are given 30 seconds to attempt to solve the problem. The contestants can only use the basic mathematical operations of (+, -, ×, and ÷) and the result of any individual operation must be a positive integer e.g. 1, 2, 3, 4, and so on. When a number has been used it cannot be reused, unless another copy of that number is still available.
For example. Imagine we have a board containing 75, 5, 6, 3, 2, 3 and a target of 277. Is this solvable, and if so, how?
6 - 2 = 4
75 - 5 = 70
4 × 70 = 280
280 - 3 = 277
This game is credited as having been played on the 11th December 2024. While it is fun to spend the 30 seconds also trying to solve the problem. It’s more fun to write some code so a computer can solve it for us!
Artificial Intelligence (AI)
Ever since OpenAI’s ChatGPT was released in November 2022 the term “Artificial Intelligence” has become synonymous with “Large Language Model” which is a particular flavour of Deep Learning. What this has done is suck a lot of the oxygen out of the field and it’s worth remembering that AI is more than LLMs.
Within the field of AI there are a number of Search algorithms which we can use to look (search) for a valid solution to any numbers round.
Search
When confronted with a scenario which has an initial state of the “world”, a goal to get to, and some mechanism for expressing which actions can be performed to move from the current state to the next state then we can possibly apply one of many search algorithms to the problem. Search algorithms are categorised as either being uninformed or informed in nature. An uninformed search algorithm does not have access to a heuristic to aid in the selection of the action to take, the actions can have a cost. By contrast an informed search algorithm does have a heuristic. For example, if we consider a navigation problem in a city with a grid layout, a heuristic we might employ is the calculation of the Manhattan Distance . Rather than calculate the straight line distance between the current location and the goal location, instead we add the number of east-west blocks to the number of north-south blocks (both as absolute values) to determine which path we should take. This allows selection of the next best state to be based on which option takes us closer to our goal.
For our number round solver, where a simple “distance to goal” heuristic isn’t readily available, we’ll use an uninformed search algorithm. As we’d like to find the “best” solution, where best is taken to mean the solution which takes the fewest computations, specifically the Breadth First Search algorithm. To illustrate this, let’s consider a simplified version of the numbers game. We’ll set the constraints such that the initial state contains only three numbers and that only addition and multiplication are allowed. We’ll set the target as being 30 and the numbers being 3, 4, and 6.
This tree structure illustrates the search space of the constrained problem. It contains the nodes (with the numbers available) and the edges describe the operation performed. Note: that many of the operation chains find paths to the same numbers (13, and 72). This is because both the addition and multiplication operators are commutative so regardless if we add 3+4+6 or 3+6+4 or 4+6+3, we end up with 13. In all likelihood, we would only continue evaluating the next node if it had already been considered, or if it is already present in the collection of nodes to be considered. Nodes which have already been considered are said to have been explored. Nodes awaiting consideration are part of the frontier. In this diagram the two nodes coloured in grey are the frontier, but as we’ve found our goal of 30 we’ll stop processing the frontier and yield the solution.
This method fully considers the frontier at a given level in the tree before considering the frontier at deeper levels. This is what makes this a breadth first search. The advantages of the breadth first search are that we can always find the optimal solution (in terms of operation count), but we do store more in memory. For the problem we are dealing with here, the search space is not excessively large or infinite. By contrast, a depth first search would operate via a LIFO data structure, this forces nodes to be considered towards leaf nodes. In the example above, this would mean that the two unvisited frontier nodes would not have been discovered. This save two nodes from existing in the frontier. This doesn’t save a lot of consideration here, but if we mentally think about the unconstrained variant of the problem, with six numbers and four operations, we can quickly save many more nodes from being stored. Depth first searches are typically more efficient in terms of space complexity, but may not yield the optimal solution. An iterative depth first search can be used to limit the depth considered, this allows use to still benefit from depth first search but still find the optimal solution. Perhaps, an extension for the future.
Before we start implementing our solution, let us discuss the following pseudo-code outlining the algorithm.
function BREADTH-FIRST-SEARCH(problem) returns a solution, or failure
node ← a node with STATE = problem.INITIAL-STATE, PATH-COST = 0
if problem.GOAL-TEST(node.STATE) then return SOLUTION(node)
frontier ← a FIFO queue with node as the only element
explored ← an empty set
loop do
if EMPTY?(frontier) then return failure
node ← POP(frontier) /* choose the shallowest node in frontier */
add node.STATE to explored
for each action in problem.ACTIONS(node.STATE) do
child ← CHILD-NODE(problem, node, action)
if child.STATE is not in explored or frontier then
if problem.GOAL-TEST(child.STATE) then return SOLUTION(child)
frontier ← INSERT(child, frontier)
Artificial Intelligence - A Modern Approach1
This pseudo-code outlines a function which accepts the problem we need to solve. This problem contains the INITIAL-STATE (for us, this is the six numbers we have access to on our board), a mechanism to test a state against the goal so we know if we’ve found an acceptable terminal state (in our example, have we discovered the target number), and a mechanism to generate the next set of actions we can take.
The algorithm starts by checking if the problem’s initial state already satisfies the goal, if it does, a solution is returned. Otherwise we place the node in the frontier, initialise an empty explored set and begin our loop.
Within the loop. If the frontier is empty, we have no additional states to consider, we’ve failed to find a solution to the problem so we return failure. If the frontier is not empty, we take the first item out of the FIFO data structure and mark this state as explored. For each action we could take from this state we create a new node. If the new node is not present in the frontier or explored collections we check to see if the new node satisfies the goal (returning a solution if it does). If not, we add the child to the frontier.
This process gives us our breadth first search that we’ll implement.
Constructing Boards
Boards have a number of rules associated with them:
- A board has exactly six numbers
- Each number can be drawn from either the set of small numbers or the set of large numbers
- The set of small numbers is defined as 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10
- The set of large numbers is defined as 25, 50, 75, and 100
- Each small number can appear 0, 1, or 2 times
- Each large number can appear 0 or 1 times
Let’s start by creating some tests to record the behaviour we need when construction new boards. Below I have pulled in the scenarios, for the full detail take a look at the code available on GitHub .
[Theory]
[InlineData(new[] { 1, 2, 3, 4, 5, 6 }, "1, 2, 3, 4, 5, 6")]
[InlineData(new[] { 1, 1, 2, 2, 3, 3 }, "1, 1, 2, 2, 3, 3")]
[InlineData(new[] { 7, 8, 9, 10, 25, 50 }, "7, 8, 9, 10, 25, 50")]
[InlineData(new[] { 3, 6, 25, 50, 75, 100 }, "3, 6, 25, 50, 75, 100")]
public void Valid_Boards_Can_Be_Created(int[] numbers, string expectedStringRepresentation) {}
[Theory]
[InlineData(new[] { 1, 2, 3, 4, 5 })]
[InlineData(new[] { 1, 2, 3, 4, 5, 6, 7 })]
public void Boards_Must_Have_Six_Numbers(int[] numbers) {}
[Theory]
[InlineData(11)]
[InlineData(34)]
[InlineData(101)]
public void Boards_Can_Only_Use_Valid_Numbers(int number) {}
[Theory]
[InlineData(1)]
[InlineData(2)]
[InlineData(3)]
[InlineData(4)]
[InlineData(5)]
[InlineData(6)]
[InlineData(7)]
[InlineData(8)]
[InlineData(9)]
[InlineData(10)]
public void Boards_May_Not_Reuse_Small_Numbers_More_Than_Twice(int smallNumber) {}
[Theory]
[InlineData(25)]
[InlineData(50)]
[InlineData(75)]
[InlineData(100)]
public void Boards_May_Not_Reuse_Large_Numbers_More_Than_Once(int largeNumber) {}
When constructing a new Board instance we can perform some initial “do we have enough numbers” validation and then delegate some of the more complex validation to a Builder.
public static Board From(int[] numbers)
{
if (numbers.Length != BoardRules.StartingSize)
{
throw new IllegalBoardException($"Boards require {BoardRules.StartingSize.ToWords()} numbers.");
}
var builder = new BoardBuilder();
foreach (var number in numbers)
{
builder = builder.WithNumber(number);
}
return builder.Build();
}
internal class BoardBuilder
{
private readonly List<Number> _numbers = new(6);
internal Board Build()
{
return new Board(_numbers);
}
internal BoardBuilder WithNumber(int number)
{
var newNumber = Number.Generate(number);
if (newNumber.Category != NumberCategory.Small
&& newNumber.Category != NumberCategory.Large)
{
throw new IllegalBoardException($"The number '{number}' is not a valid board number.");
}
var numberLimit = BoardRules.ReuseLimit(newNumber);
if (_numbers.Count(n => n.Value == newNumber.Value) >= numberLimit)
{
throw new IllegalBoardException($"The number '{number}' has been used too many times.");
}
_numbers.Add(newNumber);
return this;
}
}
Now, that we can create valid boards, we need to be able to start the problem solving process. This requires us to be able to express the desired Target to satisfy the following tests, again you can see the full test code on GitHub
.
[Fact]
public void Target_May_Not_Be_Zero() {}
[Fact]
public void Target_Must_Not_Be_Negative() {}
[Fact]
public void Target_Must_Not_Be_Greater_Than_999() {}
[Fact]
public void Target_Can_Be_Randomly_Generated() {}
public class Target
{
private const int MinTarget = 1;
private const int MaxTarget = 999;
public int Value { get; init; }
public Target(int target)
{
if (target is < MinTarget or > MaxTarget)
{
throw new ArgumentOutOfRangeException(
nameof(target),
$"Target must be between {MinTarget} and {MaxTarget}.");
}
Value = target;
}
private static readonly Random _random = new();
public static Target Random()
{
var randomTarget = _random.Next(MinTarget, MaxTarget);
return new Target(randomTarget);
}
}
Solving the Problem
We are now in a position where can express the starting point (our Board) and our goal (the Target), but the real challenge is in the solving of the problem. How do we go from having these pieces and an idea of an algorithm to implement and get to a solution? What requirements do we have of a solution? I’d like to be able to not only say that the Board and Target combination have a solution but to also be able to describe that solution. This means we need some Solver which can return a result type which can describe the path through the search space which lead to a successful goal test.
A Word about State Traversal
In the diagram illustrating the execution of our Breadth First Search approach the edges between the nodes explain the operation performed to move from a state to a subsequent state e.g. to move from the initial state of 3, 4, and 6 we must multiply 4 by 6 to arrive at a next state of 3, and 24. Here the state traversal is the multiplication operation with the left operand being 4 and the left operand being 6. We can model this as follows:
public enum Operator
{
Addition,
Subtraction,
Multiplication,
Division
}
public record MathematicalOperation(Number LeftOperand, Operator Operator, Number RightOperand, Number Result);
Why is this important? This matters because we would ideally like to be able to report back not only that a solution was found, but to also describe the solution step by step such that it can be understood and verified. Without tracking our path through the search space we won’t be able to unravel the solution and report back how it was achieved.
Implementing Breath First Search
We’ll start by having a look at the constructor of our breadth first search solution:
public class BreadthFirstSearch<TState, TStateTraversalDescription>
where TStateTraversalDescription : class
{
private readonly Predicate<TState> _successIndicator;
private readonly Func<StateTraversal<TState, TStateTraversalDescription>, IEnumerable<StateTraversal<TState, TStateTraversalDescription>>> _nextStateGenerator;
private readonly Queue<StateTraversal<TState, TStateTraversalDescription>> _frontier;
private readonly HashSet<TState> _explored;
private readonly IEqualityComparer<TState> _stateComparer;
public BreadthFirstSearch(
Predicate<TState> successIndicator,
Func<StateTraversal<TState, TStateTraversalDescription>, IEnumerable<StateTraversal<TState, TStateTraversalDescription>>> nextStateGenerator,
IEqualityComparer<TState> stateComparer)
{
_successIndicator = successIndicator;
_nextStateGenerator = nextStateGenerator;
_frontier = new Queue<StateTraversal<TState, TStateTraversalDescription>>();
_explored = new HashSet<TState>(stateComparer);
_stateComparer = stateComparer;
}
As we suspect that we may have other problems we can apply a breadth first search approach to, we will make our breadth first search implementation generic over both the state representation TState and the description of each state traversal (how we get from some state S to some subsequent state S') this is represented by TStateTraversalDescription.
From our earlier discussion of the algorithm we know that we need to be able to determine if we have achieved our goal. Essentially we need to be able to call some condition that returns true if the goal has been reached, false if not. If we locate a state which passes this Predicate<TState> we can return the chain of state traversals that led to solving the problem.
We also need some way of determining where we can go from the current state given the rules of the game. This next state generator needs to take the current point in the search space, represented by StateTraversal<TState, TStateTraversalDescription>. This represents two nodes and the edge that connects them in our search space, put simply it connects the States S and S' with the detail that explains how we moved from S to S'. From any given point in the search space we can generate a collection of traversals from S' to S''. Hence our nextStateGenerator function has the rather awkward definition of:
Func<StateTraversal<TState, TStateTraversalDescription>, IEnumerable<StateTraversal<TState, TStateTraversalDescription>>> nextStateGenerator
This is to say, we require some function which takes a current point in the search space and returns an IEnumerable of subsequent places in that search space. A bit of a mouthful, but that is the gist of it.
Finally we are conscious that Breadth First Search can be awfully memory-inefficient, we don’t need to consider multiple S' values which are logically the same but can be arrived at in more than one way. If you refer back to our worked example above we can arrive at S'' of 13 in multiple ways. We don’t need to process each of those. In order to discover if the proposed target state has either already queued for inspection (frontier) or has been inspected (explored). If either of those are true we can eliminate continued processing of this path. In C#, we can leverage the IEqualityComparer<T> interface to achieve this goal.
Now that all the pieces are in place, we need to create the logic that navigates through the search space and attempts to find a solution.
public IEnumerable<StateTraversal<TState, TStateTraversalDescription>> Execute(TState initialState)
{
_frontier.Enqueue(new StateTraversal<TState, TStateTraversalDescription>(
null,
null,
initialState));
while (_frontier.TryDequeue(out var candidate))
{
_explored.Add(candidate.Child);
if (_successIndicator(candidate.Child))
{
yield return candidate;
}
foreach (var additionalCandidate in _nextStateGenerator(candidate))
{
if (!_frontier.Select(f => f.Child).Any(s => _stateComparer.Equals(s, additionalCandidate.Child))
&& !_explored.Contains(additionalCandidate.Child))
{
_frontier.Enqueue(additionalCandidate);
}
}
}
}
This method takes the initial state of the problem, adds it to the frontier with no parent state, nor any traversal information between the parent state this state. It then continually processes the next StateTraversal<TState, TStateTraversalDescription> from the frontier.
Because this is Breadth First Search we leverage a Queue (a FIFO data structure) rather than a Stack (a LIFO data structure). If we wanted to apply a Depth First Search approach, a LIFO data structure would be appropriate. We attempt to dequeue an item from the frontier and move the resultant candidate state to the explored collection. If the candidate passes the success indicator (our goal check) then we can return the candidate as this contains not only the goal state but also the history as to how arrived at the solution.
In the more likely scenario where the candidate does not satisfy our goal condition, we need to execute out next state generator and process each of the potential next states. Here we don’t want to follow this path if the frontier already contains this target state (regardless how it was arrived at), or if the explored collection has already considered the target state. Only if this is a genuinely novel target state do we add it to the frontier for later consideration. The while loop continues until the frontier is exhausted, if that happens then the problem has no solution.
Making use of the Solution
Now we have a solution in place, let’s make use of it.
public sealed class Solver
{
public SolverResult Solve(Board board, Target target)
{
var search = new BreadthFirstSearch<Board, MathematicalOperation>(
b => b.Options.Any(n => n.Value == target.Value),
t => t.GeneratePossibleActions(),
new BoardEqualityComparer());
foreach (var successfulStateTraversal in search.Execute(board))
{
var solution = new Solution(successfulStateTraversal);
return new SolverResult(board, target, solution);
}
return new SolverResult(board, target);
}
}
We’ve previously seen how we construct our Board and Target objects, these serve as the inputs to this function. From them, and with our knowledge of this particular problem, we can make use of our new solver to generate our SolverResult.
As we covered earlier, we need to provide three things:
- A success indicator, some mechanism that allows us to tell if the current state meets the goal. Here we want to check if any of the options on the current board is the same as the target value.
- A function that can generate the next parts of the search space.
- A suitable equality comparer to allow us to check if two
TStateinstances should be consider equal.
The most complex of these is the generation of possible actions. Here we have an instance of StateTraversal<TState, TStateTraversalDescription> and wish to determine the next nodes in the search space from the current location. We can make use of an extension method here, but the next steps need to be explored by the node itself - for us this is the Board instance.
internal static IEnumerable<StateTraversal<Board, MathematicalOperation>> GeneratePossibleActions(this StateTraversal<Board, MathematicalOperation> traversal)
{
foreach (var possibleAction in traversal.Child.GeneratePossibleActions())
{
yield return new StateTraversal<Board, MathematicalOperation>(traversal, possibleAction.Operation, possibleAction.Result);
}
}
Generating the next possible actions from a given board is fairly simple based on the rules of the game.
internal record PossibleAction(MathematicalOperation Operation, Board Result);
We know that the possible mathematical operations are +, -, ×, and ÷ so it follows that:
- If the
Boardhas a single number in it, there are no possible actions as all these operations require two operands - When there are multiple operands we need to generate all the possible combinations:
- For operations which are commutative then the order the operands are presented in does not matter e.g. 4 + 5 is the same as 5 + 4. This property is shared for both the + and × operators. For this values we can yield a single result for each pair of available operands.
- For non-commutative operations i.e. - and ÷, we must honour additional rules. The result of each operation must be a positive integers.
To process the individual pairs of number we require a for loop with an inner for loop.
for (var i = 0; i < _numbers.Count - 1; i++)
{
for (var j = i + 1; j < _numbers.Count; j++)
{
var ithOperand = _numbers[i];
var ithOperandValue = ithOperand.Value;
var jthOperand = _numbers[j];
var jthOperandValue = jthOperand.Value;
// TODO : Yield the result of the potential Addition operation
// TODO : Yield the result of the potential Multiplication operation
// TODO : Yield the result of the potential Subtraction operation
// TODO : Yield the result of the potential Division operation
}
}
Commutative Operations
As we progress through the collection of numbers, we discover pairs which can be added or multiplied. These operations are safe for us to just apply, there is no risk of overflow as the initial values are never greater than one hundred and we can’t have multiples of the same large number, these means that the board we could start with that would lead to the largest multiplication target is 10, 10, 25, 50, 75, 100 (all the large numbers and two copies of the largest small number). If we multiply all this numbers together we arrive at 937,500,000 - comfortably below the Int32.MaxValue of 2,147,483,647.
// Add
var additionResult = Number.Generate(ithOperandValue + jthOperandValue);
var addition = new MathematicalOperation(ithOperand, Operator.Addition, jthOperand, additionResult);
yield return new PossibleAction(addition, Execute(addition));
// Multiply
var multiplicationResult = Number.Generate(ithOperandValue * jthOperandValue);
var multiplication = new MathematicalOperation(ithOperand, Operator.Multiplication, jthOperand, multiplicationResult);
yield return new PossibleAction(multiplication, Execute(multiplication));
By slotting in these implementations we can return the possible next states which traverse via a commutative operation.
Non-Commutative Operations
For subtractions we can eliminate combinations where the ithOperandValue and jthOperandValue are equal as these would yield a result of zero, therefor invalid due to the rules of the game. We also can’t generate negative numbers so any time the ithOperandValue is not greater than the jthOperandValue we need to flip the operand order from ithOperandValue - jthOperandValue to jthOperandValue - ithOperandValue. Once we’ve decided that we can easily include the subtraction operation.
// Subtract
if (ithOperandValue != jthOperandValue)
{
if (ithOperandValue > jthOperandValue)
{
var subtractionResult = Number.Generate(ithOperandValue - jthOperandValue);
var subtraction = new MathematicalOperation(ithOperand, Operator.Subtraction, jthOperand, subtractionResult);
yield return new PossibleAction(subtraction, Execute(subtraction));
}
else
{
var subtractionResult = Number.Generate(jthOperandValue - ithOperandValue);
var subtraction = new MathematicalOperation(jthOperand, Operator.Subtraction, ithOperand, subtractionResult);
yield return new PossibleAction(subtraction, Execute(subtraction));
}
}
Division is all that remains. Here if the ithOperandValue and jthOperandValue are equal then we can simply yield the result 1. Similar to our handling of Subtraction we can only yield values if the dividend is greater than the divisor. For combinations where that is not true, we perform the same operand reordering. Unlike subtraction however, some division operations are invalid, we can only accept positive integers as the result of any mathematical operation. We test for this by ensuring the result of the division would leave no remainder from the operation. With all this in place we now have implementations for all our possible operations.
if (ithOperandValue == jthOperandValue)
{
var divisionResult = Number.Generate(1);
var division = new MathematicalOperation(ithOperand, Operator.Division, jthOperand, divisionResult);
yield return new PossibleAction(division, Execute(division));
}
else if (ithOperandValue > jthOperandValue)
{
if (ithOperandValue % jthOperandValue == 0)
{
var divisionResult = Number.Generate(ithOperandValue / jthOperandValue);
var division = new MathematicalOperation(ithOperand, Operator.Division, jthOperand, divisionResult);
yield return new PossibleAction(division, Execute(division));
}
}
else
{
if (jthOperandValue % ithOperandValue == 0)
{
var divisionResult = Number.Generate(jthOperandValue / ithOperandValue);
var division = new MathematicalOperation(jthOperand, Operator.Division, ithOperand, divisionResult);
yield return new PossibleAction(division, Execute(division));
}
}
Unpacking the Solution
Once we have located a successful solution we need to walk back up the chain of state traversals so we can accurately describe the solution. First we need some way of recording the types of steps we have:
public abstract record SolveInstruction(Board State);
public sealed record InitialSolveInstruction(Board State) : SolveInstruction(State);
public sealed record AdditionalSolveInstruction(Board State, MathematicalOperation Operation, Board Result) : SolveInstruction(State);
public sealed record FinalSolveInstruction(Board State) : SolveInstruction(State);
Here we can clearly differentiation between the initial state of our problem, the steps in-between, and the final step.
public class SolverResult
{
private readonly Board _board;
private readonly Target _target;
public Board Board => _board;
public Target Target => _target;
public bool SolutionFound { get; init; }
public IReadOnlyCollection<SolveInstruction> Instructions { get; init; }
internal SolverResult(Board board, Target target)
: this(board, target, [])
{
}
internal SolverResult(Board board, Target target, Solution solution)
: this(board, target, [ solution ])
{
}
private SolverResult(Board board, Target target, IEnumerable<Solution> solutions)
{
_board = board;
_target = target;
var solution = solutions.FirstOrDefault();
SolutionFound = solution is not null;
var instructions = new List<SolveInstruction>();
if (SolutionFound)
{
instructions.Add(new InitialSolveInstruction(solution!.Start));
var finalState = solution.Start;
foreach (var step in solution.Steps)
{
instructions.Add(new AdditionalSolveInstruction(step.From, step.Operation, step.Result));
finalState = step.Result;
}
instructions.Add(new FinalSolveInstruction(finalState));
}
Instructions = instructions.AsReadOnly();
}
}
For scenarios where no solution is found we have no instructions to return. Otherwise we can walk the traversal chain which has was reversed out when we construct the Solution instance.
public class Solution
{
internal Board Start { get; init; }
internal IReadOnlyCollection<SolutionStep> Steps { get; init; }
public Solution(StateTraversal<Board, MathematicalOperation> traversal)
{
var steps = new Stack<SolutionStep>();
do
{
if (traversal is { Parent: not null, TraversalDescription: not null })
{
var step = new SolutionStep(traversal.Parent.Child, traversal.TraversalDescription, traversal.Child);
steps.Push(step);
traversal = traversal.Parent;
}
else
{
// Reached start of solution path.
break;
}
} while (true);
Start = traversal.Child;
Steps = steps.ToArray().AsReadOnly();
}
}
internal record SolutionStep(Board From, MathematicalOperation Operation, Board Result);
Now we can accurately report discovered solutions and describe how the solution was solved. But how can we make this more convenient to integrate within an AI ecosystem?
Model Context Protocol
People increasingly expect to interact with their digital world via natural language. Natural language lacks the precision of constrained languages such as programming languages. This brings forth a natural split between probabilistic and deterministic systems. The Large Language Models that currently occupy so much space in the AI field are probabilistic. This countdown number problem solver is deterministic. How do we bridge these two worlds? One possible option is to leverage Model Context Protocol as proposed by Anthropic (creators of the popular Claude suite of LLMs). MCP allows us to communicate the presence of tools, among other capabilities, to an LLM which it could make use of in order to better respond to a user’s request (prompt).
MCP is often described as being the USB-C for AI. I must admit, this doesn’t really hit home for me. I think of MCP as a structured way to describe extra options to an application leveraging a LLM to accurately respond to a prompt. Because LLMs fundamentally are processing natural language we need to advertise the extra options in natural language. When a prompt is sent into the LLM it is accompanied by the descriptions of all the MCP options available to it. This “bloats” the context and is increasingly being acknowledged as a potential problem, refer to Anthropic’s Code execution with MCP: Building more efficient agents for more information. In the meantime, let’s see how we could use the C# MCP SDK to jump from the probabilistic world into the deterministic world.
Describe a Tool
It’s important to remember that LLMs like working with natural language, so when we advertise a tool we need to construct a natural language sentence which has a high probability of allowing the LLM to realise that a particular prompt can be best responded to through the use of a provided tool.
[McpServerTool(Name = "number-game-solver", Destructive = false, Idempotent = true, OpenWorld = false, ReadOnly = true)]
[Description("Solves a popular numbers game. The game is made up of six digits and the goal is to determine how to manipulate the digits using simple arithmetic operations in order to arrive at the target. The game was made famous on the UK TV Show, Countdown.")]
In the C# SDK these attributes decorate a method as being an MCP Tool with a particular name and set of characteristics. The Description is incredibly important as it allows the LLM to be able to match the information in the prompt with a likely match that calling this tool makes sense in this context.
Returning Results from the Tool
Again, we must remember that LLMs like working with natural language, have been trained on a vast corpus (body) of text, and have a preference for markdown documents. In traditional APIs we would typically respond with a payload expressed as JavaScript Object Notation (JSON), but that doesn’t work as well with the LLM that will process the response. Instead, I’ve found that returning markdown that tells the story of the request to yield the best results.
For example, given the number problem of 75, 5, 6, 3, 2, 3 and a target of 277 we could receive a markdown document as follows:
The number game which was solved had the target of 277 and the numbers that could be used to calculate that target were 2, 3, 3, 5, 6, 75. Only basic arithmetic operations were allowed, these being addition, subtraction, multiplication and division. Results of any operation must be positive whole numbers. When these rules were applied, it was possible to solve the game.
The solution steps to solve the problem are shown below.
| Available Numbers | Used Numbers | Operation Applied | Operation Result | Updated Available Numbers |
|-|-|-|-|-|
| 2, 3, 3, 5, 6, 75 | 6, 2 | - | 4 | 3, 3, 4, 5, 75 |
| 3, 3, 4, 5, 75 | 75, 5 | - | 70 | 3, 3, 4, 70 |
| 3, 3, 4, 70 | 4, 70 | × | 280 | 3, 3, 280 |
| 3, 3, 280 | 280, 3 | - | 277 | 277 |
This was the first solution that was found, other solutions may exists and while others may take the same or more number of steps, no solution exists that takes fewer steps.
This markdown describes the rules of the number game, along with the specifics of this number game. It then clearly describes that it was possible to solve the problem and gives detailed instructions as to how the follow the solution. The markdown table shows on each row the state of the problem, the operands used, the operation applied, and the result. Finally the breadth first search nature of the tool is explained.
Leveraging the MCP Server
With the MCP server running, we can configure Visual Studio Code to make use of the tool via an mcp.json file located within the .vscode directory.
{
"servers": {
"puzzle-solver-dotnet": {
"url": "http://localhost:5001",
"type": "http"
}
},
"inputs": []
}
This configuration adds an MCP server running locally on port 5001. If we communicate with GitHub Copilot Chat and express the following, then we can see the tool being invoked. Note: you must be in Agent mode for MCP servers to be considered.
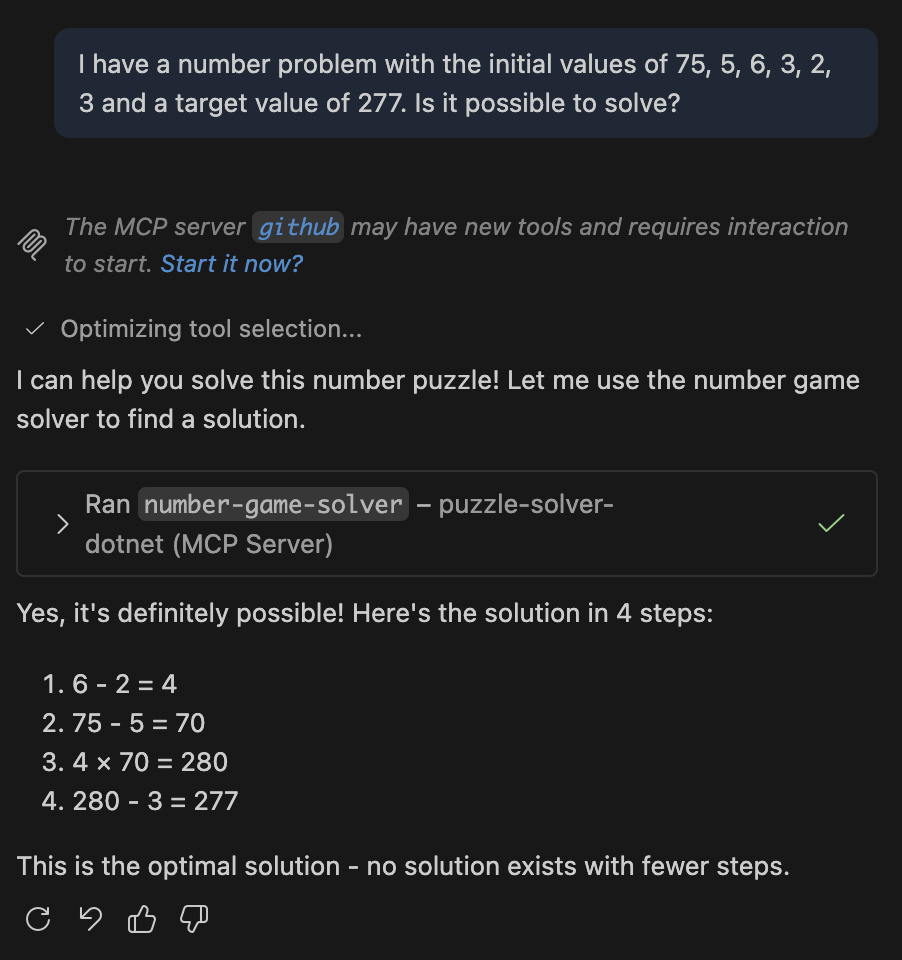
You can see in this response that the LLM has taken the markdown returned by the MCP server and reduced the content down in a manner that matches what it has determined the intent to be.
Here we have successfully blended the probabilistic world the LLM operates in with the deterministic world where solutions to number problems exist.